报告题目 (Title)：On the sine polarity and the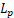 
-sine Blaschke-Santaló inequality.
中文标题：正弦极体和 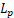-正弦Blaschke-Santaló不等式。
报告人 (Speaker)：李爱军（浙江科技大学）
报告时间 (Time)：2024年4月18日(周四) 11:10
报告地点 (Place)：校本部GJ303
邀请人(Inviter)：席东盟、李晋、张德凯、吴加勇
报告摘要：This talk is dedicated to study the sine version of polar bodies and establish the 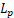-sine Blaschke-Santaló inequality for the 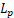-sine centroid body. The 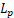-sine centroid body
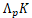for a star body K is a convex body based on the 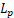-sine transform, and its associated Blaschke-Santaló inequality provides an upper bound for the volume of 
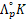, the polar body of 
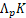, in terms of the volume of K. Thus, this inequality can be viewed as the “sine cousin” of the
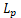Blaschke-Santaló inequality established by Lutwak and Zhang. As 
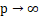, the limit of 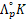becomes the sine polar body 
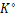and hence the 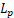-sine Blaschke-Santaló inequality reduces to the sine Blaschke-Santaló inequality for the sine polar body. The sine polarity naturally leads to a new class of convex bodies 
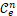, which consists of all origin-symmetric convex bodies generated by the intersection of origin-symmetric closed solid cylinders. Many notions in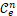are developed, including the cylindrical support function, the supporting cylinder, the cylindrical Gauss image, and the cylindrical hull. Based on these newly introduced notions, the equality conditions of the sine Blaschke-Santaló inequality are settled.